InThinking Subject Sites

Subscription websites for IB teachers & their classes

Find out more


Sitemap
Recommendations
Other subjects
Brochure

Disclaimer: InThinking subject sites are neither endorsed by nor connected with the International Baccalaureate Organisation.

Student access tools
 You need to log-in or subscribe in order to use Student access.

A2 activity: Collisions

Whether in person or online, to understand collisions you will need to observe some taking place (probably involving balls on a track). You will then be able to distinguish between elastic and inelastic collisions, model collisions with Algodoo and solve collision problems using conservation of kinetic energy and momentum.

Need to know

Doing this at home?

The first part of this activity uses video analysis and the rest Algodoo, both possible to use at home. You will need some small balls like marbles and something to use as a track. Most plastic rulers have a groove in them - this works well.

Elastic collisions

Observations

  • Fix a short section of track onto the table with blutack
  • Make sure it is horizontal by placing a ball on it.
  • Using LoggerPro analyse the motion of two balls colliding. It is simplest to start with one ball stationary and the other moving.

If you can't remember how to use video analysis here is a video.

  • Measure the velocity of each ball before and after the collision.
  • Is momentum conserved? If not why not?
  • Is KE conserved? If not why not?
  • Is the total energy conserved?
  • Try a collision with both balls moving and again measure velocities to determine if momentum and KE are conserved.

Elastic collisions

An elastic collision is one in which both momentum and kinetic energy are conserved.

Remember momentum is only conserved if the balls are isolated, this is a problem in the lab (as you have probably noticed) since the balls interact with the track. To eliminate the track we need to switch off gravity or remove friction and we can only do that in a simulation.

If two balls collide without losing any KE we say they are perfectly elastic, this depends on the material of the ball.

  • A steel ball is quite elastic but a Plasticine ball isn't, why do you think this is the case?

Elastic Collision between identical balls

First we will look at the simplest case of 1 ball hitting another that is stationary.

We don't know what will happen after the collision so let's say it's something like this:

  • Apply the principle of conservation of momentum to the collision. Both balls have mass m.
  • Use conservation of KE to write a second equation.
  • Square the first equation and use both equations to show that either v1 or v2 must = 0
  • Why can't v2 = 0?
  • Show that v2 = v

Now let's try with 2 balls moving.

Again we will assume some result.

  • Apply the principle of conservation of momentum to the collision. Both balls have mass m.
  • Use conservation of KE to write a second equation.
  • Show that the only possible solution is if the velocities swap.

Inelastic collisions

An inelastic collision is one in which only momentum is conserved.

Sticky collisions

There are many possible outcomes of an inelastic collision. One of those is when the bodies stick together (coalesce).

  • Show that in this situation the final velocity = 1/2 the initial velocity
  • If the balls have mass = 1kg and the initial velocity is 1 ms-1, calculate the loss in KE.

Explosions

Momentum is also conserved in explosions.

  • Show that the velocity of the moving ball = 2ms-1.
  • Calculate the  gain in KE.

Modelling in Algodoo

First we will consider a ball bouncing on the ground. Draw a circle some height above the ground and run the simulation so the ball bounces.

  • Is KE conserved? How can you tell?
  • Is momentum conserved? Why not? (oops I suppose you know it's not conserved now)

Change the material of the ball by choosing e.g. rubber in the materials options and observe the effect.

Restitution

The coefficient of restitution is defined as the ratio of speed after / speed before. If this is 1 then the material is perfectly elastic. Adjust the coefficient of restitution in "materials".

  • Why does the ball still lose KE?

Try bouncing the ball off a block of material with restitution = 1.

2 body elastic collisions in 1D

  • Place one ball on the ground (still in Algodoo) and make it restitution = 1 and friction = 0 and mass = 1 kg.
  • Switch off air resistance.
  • Clone the ball and place the clone also on the ground.
  • Give the first ball a velocity of 1 ms-1 along the ground by using the slider in "velocities"
  • Display the momentum and KE of each ball by choosing "information" and dragging the box to one side.
  • Are momentum and KE conserved now? If not then something is wrong, try to work out what.

Try different elastic collisions with different size balls and different velocities. you could also try making a sort of newtons cradle without the cradle.

2 body inelastic collisions in 1D

To make inelastic collisions change the restitution to something less than 1

  • Are momentum and KE conserved now?

Try making restitution of each ball 0 and adding a bit of attraction (0.02 Nm2kg-2) so the balls stuck together.

To make an explosion set the attraction to a negative value (you have to this by typing as the slider won't go below 0)

  • Check to see if momentum is conserved.
  • Why don't the KE's cancel out like the momenta?

2D collisions

To make collisions in 2D switch off gravity and delete the ground.

First we will consider a perfectly elastic collision.

  • Apply the principle of conservation of momentum to the collision. You can apply it in the same way as you did in 1D but this time you must use vector notation.
  • Use the fact that KE is conserved to generate an equation relating the velocity vectors.

Draw a triangle of vectors to represent 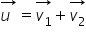     stack u subscript blank with rightwards arrow on top equals stack v subscript 1 with rightwards arrow on top plus stack v subscript 2 with rightwards arrow on top

Conservation of KE leads to the equation u2 = v12 + v22 what does this imply about the triangle?

Test this out by performing collisions in Algodoo and with balls on the table.

Are the collisions perfectly elastic in this pool game?

What would the game of pool be like if KE was conserved?

Summary

Assess yourself

Now know

For students with access to StudyIB:

Momentum 2

Olympiad 2

All materials on this website are for the exclusive use of teachers and students at subscribing schools for the period of their subscription. Any unauthorised copying or posting of materials on other websites is an infringement of our copyright and could result in your account being blocked and legal action being taken against you.