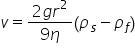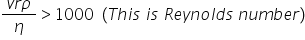In this section we will make extensive use of the PhET simulation Fluid pressure and flow which is where the animations come from.
Consider the fluid flowing in the pipe shown below:
The red dots represent particles of liquid but the pipe is full.
- Does the velocity change (think of the continuity equation)?
- As the liquid goes uphill what happens to the PE of the particles?
If the liquid is gaining energy work must be done.
Consider this more complicated situation
- Why does the velocity increase?
- What energy changes are taking place?
- Is work done on the water?
We can see that the energy increases as the water flows along the pipe so work must be done. Let us analyse the situation in more detail.
First we must realise that something must be pushing the liquid, like a pump or piston.
The animation is a bit rough but hopefully you get the point that to make the liquid flow you need to increase the pressure.
![]()
Consider this case:

Pressure from the water outside the pipe pushes on each end but the pressure at the bottom is bigger forcing the liquid through the pipe.
- Why does the liquid move further at the top end?
- If the velocity in the lower section is constant what can you deduce about the Pressure inside this section of pipe and the pressure outside?
- Write an expression for the work done on the water by the force at the bottom end.
At the top end the water moves in the opposite direction to the force, F2.
- What can you deduce about the works done at the top end?
- Show that:
Net work done, W = P1A1x1 - P2A2x2
- If V = Ax = m/ρ show that
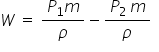
- Write an expression for the change in KE and PE energy when the fluid flow up the hill.
- The work done will equal the gain in energy, by equating these expressions show that:
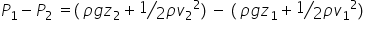
This leads to the Bernoulli equation:
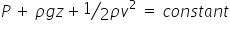
Note that this only applies along a streamline.
Example:
Water flows into a pipe of radius 2 cm at a rate of 100 cm3s-1 at a pressure of 500 kPa.
- Calculate the velocity of the water.
The pipe is connected to a thicker pipe of radius 5 cm that is 4m above the height of the first one.
- Calculate the velocity in the second pipe.
- Calculate the pressure of the water in the top pipe.
Use this GeoGebra simulation to check your answers (note that the radius and height are not the same scale)







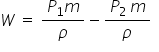
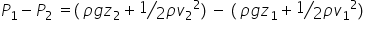
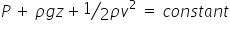
 Note that because the top and the bottom are open, the pressure is the same as atmospheric pressure at both openings.
Note that because the top and the bottom are open, the pressure is the same as atmospheric pressure at both openings.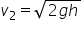
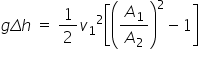
 The streamline shown ends in the tube with zero velocity. The pressure here is called the stagnation pressure.
The streamline shown ends in the tube with zero velocity. The pressure here is called the stagnation pressure.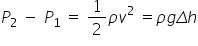
 Explain what causes the difference in fluid level.
Explain what causes the difference in fluid level.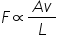
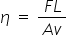
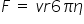
 Consider the situation of the ball ball shown. It has density ρs and is falling at terminal velocity through a fluid of density ρf.
Consider the situation of the ball ball shown. It has density ρs and is falling at terminal velocity through a fluid of density ρf.