Circular Motion
Aims
- Introduce the quantities of circular motion.
- Understand that if a body moves in a circle there must be an acceleration towards the centre and therefore an unbalanced force towards the centre.
- Accept that centripetal force = mv2/r and use this equation to solve simple problems.
- Identify the centripetal force in a variety of examples.
TOK
This is another example of perception vs physical reality. One's feeling when you go round a corner in a car is that you are being pushed outwards however physics says the force is inwards.
NOS
We can conclude that if a body moves in a circle there must be a force towards the centre by considering energy changes or the change of velocity over a short displacement. Two different perspectives give the same outcome.
Utilisations
Fairground rides, cars going around bends, looping the loop.
Notes
A common misconception here is that the centripetal force is another force like weight, tension, friction etc. however it isn't another force it is the name of the resultant unbalanced force towards the centre. In the case of a satellite this would be gravity.
Its also a good opportunity to reinforce newtons 3rd law here. See if students can identify where the other force is.
It's not really necessary to derive the formula for centripetal acceleration but I always like to do it anyway.
Resources
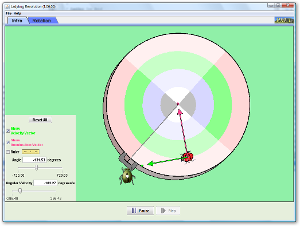
The ladybug revolution
This simulation is very useful if you do the rotational mechanics option but also can be used here to show how friction keeps the ladybug (ladybird in UK English) moving in a circle.
Here is an idea how to use a screenshot (on a smartboard) from the simulation to show that the change in velocity points towards the centre.
Video
Some great examples of circular motion on YouTube. Here are a couple: