New student resources
Wednesday 17 August 2016
 It´s not quite ready yet but I thought I´d write about what I have been constructing for the past 6 months, it´s a new student site designed to aid revision and hone problem solving skills. Eventually it will be a separate subscription site for students but in the first instance it will be free to all students in subscribing schools.
It´s not quite ready yet but I thought I´d write about what I have been constructing for the past 6 months, it´s a new student site designed to aid revision and hone problem solving skills. Eventually it will be a separate subscription site for students but in the first instance it will be free to all students in subscribing schools.
I have attempted to reduce the course into; things to remember, concepts to understand and skills to develop. The remembering is mainly definitions and laws so this can be handled in text and pictures. Concepts are more difficult and require explanation so I have used video with plenty of animations. Skills require practice so there are lots of questions.
Phase 1 (almost finished) is over 300 videos of maximum length 1 minute explaining each concept of the course. This starts easy enough but after a while the understanding of a concept requires understanding of another, anyway we´ll see how it goes. Associated with each video there will be a set of questions. An example page is shown below.
Phase 2 (just started) is a much more interesting use of technology to create learning networks to help students to develop problem solving skills.
So here is a taster:
The simple pendulum
Simple harmonic motion is when:
Specifically small amplitude swings
Which of the following are SHM
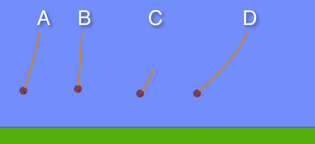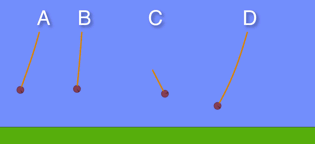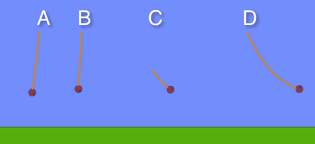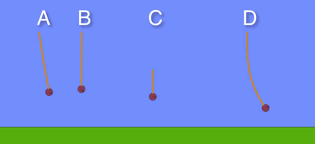
B has small amplitude so is appproximately SHM
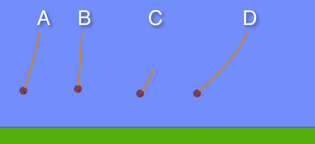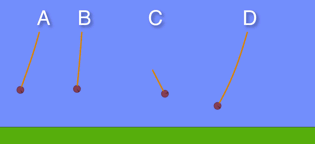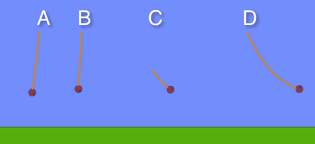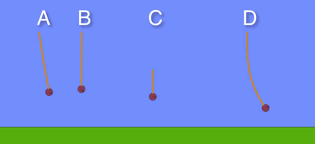
Which pendulum has the biggest frequency?
C completes most cycles per unit time
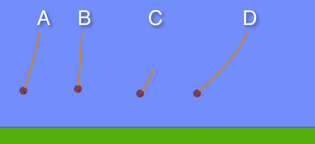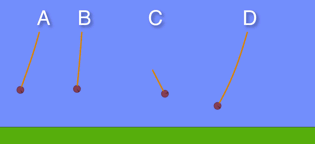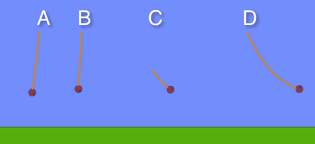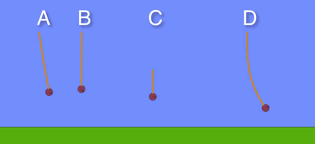
Which pendulum has the longest time period?
D takes the longest time to complete a full cycle
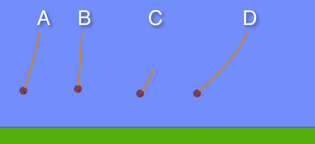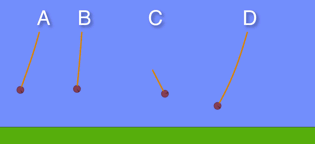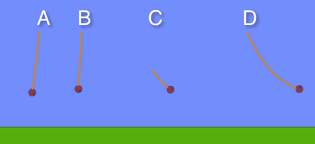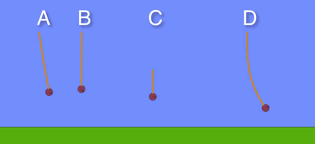
Which pendulum has the largest amplitude?
The distance from the equilibrium position to maximum displacement is largest in D
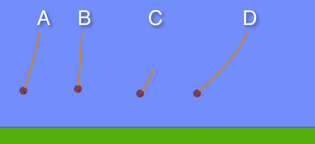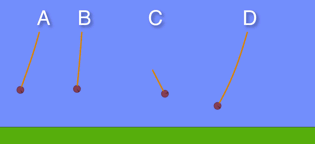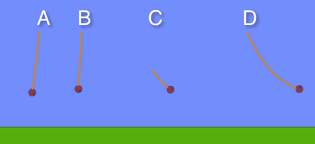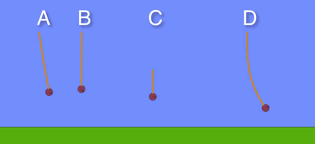
In which pendulum will the tension in the string reach the largest value?
This is a tricky one.
The tension is greatest at the bottom of the swing and depends on velocity2/radius. D has the highest velocity but also the longest radius. However the higher velocity outweighs the larger radius so D has the biggest tension.
The simplest way to answer this is to use your intuition, which would be the most difficult to hold?
The pendulum below is swinging to the left
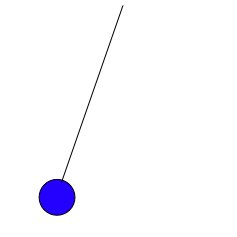
The direction of the resultant force is
The force will act towards the equilibrium position
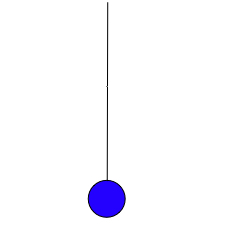
The pendulum below is at the furthest point to the left
The resultant force is
Restoring force is proportional to displacement and directed towards the equilibrium position.
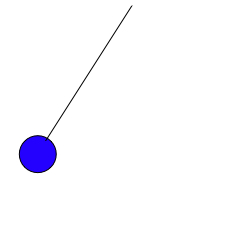
The pendulum below is moving to the right
The resultant force is
The pendulum bob is moving along the arc of a circle so there is a force towards the centre.
The pendulum bob below is at rest

The resultant force is
Forces are balanced
If the pendulum amplitude is very small we can assume that
In deriving the equation we assume that T = mg at the equilibrium position
The equation for the time period of a simple pendulum is
If the time period of a pendulum is 0.5s, The length of the string is increased by a factor 4 the time period will be
T is proportional to √4 so will be 2x bigger
The equation for the time period of a simple pendulum is
The time period of a pendulum is 0.5s, if the pendulum is taken to the moon the time period will be
g on the moon is about 1/6 that on Earth
T is proportional to 1/√g so T = 0.5 x √6
The equation for the time period of a simple pendulum is
Ihe time period of a pendulum is 0.5s, if the mass is doubled the time period will be
The time period does not depend on mass.
The equation for the time period of a simple pendulum is
The frequency of a pendulum is 1 Hz The length of the string is increased by a factor 4 the frequency will be
f= 1/T so f is proportional to 1/√L so if L is x4, f will be x 1/2

