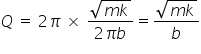Comments (damped harmonic motion)

Friday 26 February 2021

When someone leaves a comment on a page I always try to answer as quickly as possible, usually within a couple of hours. Sometimes you ask a difficult question that takes a bit more time, This week Yang Bing asked a difficult question.

"Hi Chris, for the equation of 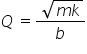 Q space equals fraction numerator space square root of m k end root over denominator b end fraction ,could you show me the derivation of that? I found it from your Book in topic of Q factor, damping harmonic motion."

Hmm, I have no idea but I will try to find out.

Google didn't help, all the maths was too difficult so I tried to work it out myself. It took some time but here it is.

From the definition :

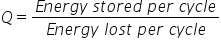
Q equals fraction numerator E n e r g y space s t o r e d space p e r space c y c l e over denominator E n e r g y space l o s t space p e r space c y c l e end fraction

The equation for the displacement of a body oscillating with damped harmonic motion is:

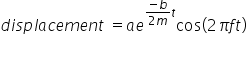
d i s p l a c e m e n t space equals a e to the power of fraction numerator negative b over denominator 2 m end fraction t end exponent cos left parenthesis 2 pi f t right parenthesis

Sorry, there is a typo in the text book, I missed ot the 2 in -b/2m.

Energy is proportional to displacement2 so the energy at t = 0 is proportional to

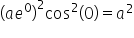
open parentheses a e to the power of 0 close parentheses squared cos squared left parenthesis 0 right parenthesis equals a squared

If the time period is T the energy after one cycle is

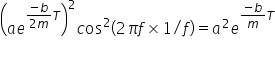
open parentheses a e to the power of fraction numerator negative b over denominator 2 m end fraction T end exponent close parentheses squared c os squared left parenthesis 2 pi f cross times 1 divided by f right parenthesis equals a squared e to the power of fraction numerator negative b over denominator m end fraction T end exponent

But

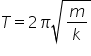
T equals 2 pi square root of m over k end root

So the energy after one cycle is

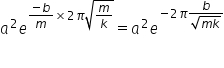
a squared e to the power of fraction numerator negative b over denominator m end fraction cross times 2 pi square root of m over k end root end exponent equals a squared e to the power of negative 2 pi fraction numerator b over denominator square root of m k end root end fraction end exponent

The energy lost is therefore

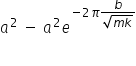
a squared space minus space a squared e to the power of negative 2 pi fraction numerator b over denominator square root of m k end root end fraction end exponent

Substituting into the equation for Q

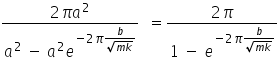
fraction numerator 2 pi a squared over denominator a squared space minus space a squared e to the power of negative 2 pi fraction numerator b over denominator square root of m k end root end fraction end exponent end fraction space space equals fraction numerator 2 pi over denominator 1 space minus space e to the power of negative 2 pi fraction numerator b over denominator square root of m k end root end fraction end exponent end fraction

This is of the form

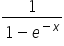
fraction numerator 1 over denominator 1 minus e to the power of negative x end exponent end fraction

This is where my memory of A'level maths fails but I do remember something called a Laurent series which is used to expand functions and show the value they tend to when x is small. The Q value is only relevant for examples of light damping so this seems to be the way to go, unfortunately I don't remember how to do this but no problem Wolframalpha can do it for me.

Not sure what "series expansion at x = 0 means but let's go with it anyway.

This shows that for small values of x 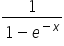 fraction numerator 1 over denominator 1 minus e to the power of negative x end exponent end fraction tends to 1/x.

Just to be sure we can plot the two functions in GeoGebra.

Looks good :-)

So

Q space equals space 2 pi space cross times space fraction numerator square root of m k end root over denominator 2 pi b end fraction equals fraction numerator square root of m k end root over denominator b end fraction

Modifications in 2022
3 Mar 2021
In page written tasks (improved feature).
20 Feb 2021